Cómo encontrar el área de un triángulo isósceles

Matemáticas, y geometría en particular, segúnsondeos de escolares, una de las lecciones menos amadas, y todo porque te hacen aprender una gran cantidad de fórmulas que en la vida el 90% de los adultos actuales no han encontrado aplicación práctica. Pero, por un minuto, aprendemos fórmulas, resolvemos problemas, hacemos ecuaciones no por el hecho de que puedan sernos útiles en la vida, sino porque desarrolla el pensamiento y la lógica. Incluso los antiguos sabios griegos decían que el intelecto humano puede medirse por el conocimiento de las ciencias matemáticas. Y desde que decidió familiarizarse con la aplicación de las fórmulas para un triángulo isósceles, nos tomamos a nosotros mismos y leemos el artículo completo.
Antes de comenzar a responder la pregunta de cómo encontrarel área de un triángulo isósceles y vaya a la parte práctica del artículo, donde se dan las fórmulas y los cálculos, denotemos el concepto mismo para nosotros mismos. Un triángulo isósceles es un triángulo en el que dos de los tres lados tienen la misma longitud, llamados lados laterales. En el caso de un triángulo regular, donde todos los lados son iguales, también se considera isósceles, pero viceversa, cuando un triángulo isósceles se considera correcto, es falso.
Los lados del triángulo se deben designar, lo haremos de esta manera, como se muestra en la siguiente imagen, donde: a - lados, base b y altura h.
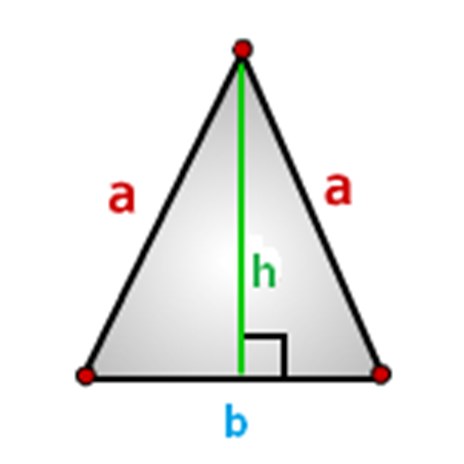
Cómo calcular el área de un triángulo isósceles, fórmulas.
Después de hacer la notación de altura, lados y ángulo, podemos comenzar a resolver el problema.
Para empezar, determinaremos lo que sabemos.
Si la altura y el fondo - entonces la fórmula clásica (* - signo de multiplicación):
S = ½ * b * h
Vamos a sustituir, por ejemplo, los números donde: h = 16, b = 18, obtenemos lo siguiente:
S = ½ * 18 * 16 = 9 * 16 = 144;
El área de un triángulo isósceles es S = 144 cm2
Hay otras fórmulas que nos ayudaránen cómo saber el área de un triángulo isósceles. Una de esas fórmulas es el método de Heron. No escribamos una fórmula compleja, tomamos, por una base, una abreviatura:
S = ¼ b √4 * a2-b2
Está claro que b es la base, y - lados iguales. La fórmula es adecuada en el caso donde la altura h es desconocida.
Sustituyendo los valores, deje a = 6, b = 3, obtenemos lo siguiente:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Puede usar para calcular el área igual a los lados del triángulo y el ángulo entre los lados:
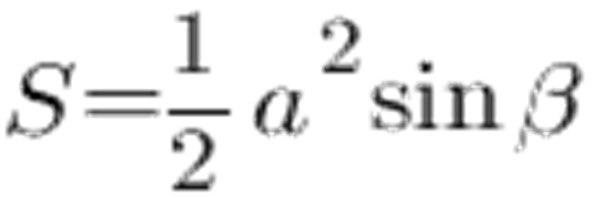
De acuerdo con la tabla sinusoidal, el ángulo a 45 ° es igual a 0.7071, el lado a, y que sea 6 cm, obtenemos lo siguiente:
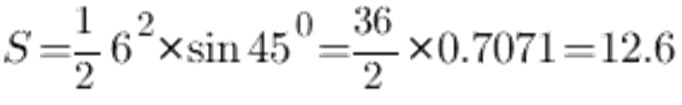
Como resultado, el área de un triángulo isósceles es de 12.6 cm2.
También hay formas de calcular el área, incluyendoincluso en el caso de un triángulo isósceles, pero son bastante complicados y no se aplican a los cálculos "elementales", como los dados anteriormente, en la noción de matemática compleja. Y no vale la pena hablar de cosas que incluso los maestros con experiencia no entenderán.
Entonces, puedes respirar con alivio, en esteun pequeño curso de geometría para encontrar el área de un triángulo isósceles se considerará completo, y el conocimiento obtenido como resultado de la lectura del artículo se aprende por "cinco".